a quien no le gustaria resolver las siguientes congruencias de la manera mas rapida y facil posible
por suerte existe una herramienta atribuida a hensel llamado el lema de hensel que nos va a ayudar a resolver este tipo de congruencias mucho mas facil y rapido omitiendo muchos calculos inncesesarios por lo tanto el lema dice lo siguiente
si asi de facil es entenderlo sinceramente busque en muchos sitios web y en ninguno pude encontrar una forma clara de demostracion por lo que buscando en sitios en el idioma ingles pude encontrar por fin una forma clara en como se demuestra por lo tanto vamos a partir de lo siguiente
primero tomamos un polinomio con las siguientes caracteristicas
lo que queremos lograr esque cuando tengamos valores que son soluciones a un polinomio congruente con la potencia de un cierto numero primo usar esos datos para obtener soluciones a potencias cada vez mas y mas altas por lo tanto ahora vamos a añadir otra propiedad
donde i es un numero entero es posible que sea negativo pero a mi me gusta mas ponerle la condicion de ser positivo usted sera quien decida que signo le pondra dependiendo de sus necesidades por lo tanto vamos a usar el polinomio de taylor y a usarlo de la siguiente forma para seguir con la demostracion
ahora acomodando se obtiene lo siguiente
ahora usando la notacion de aritmetica modular lo anterior se puede reescribir como
ahora si tomamos en cuenta lo siguiente
relacionando este dato con donde quedamos en la demostracion todo se reduciria a lo siguiente
ahora lo que aremos sera nadamas acomodar y sustituir la siguiente imagen ya es la ultima
muchas gracias por su atencion siganos en facebook y twitter como MateVlog Muchas Gracias por ver
Bibliogfafia:
Wikipedia:https://en.m.wikipedia.org/wiki/Hensel%27s_lemma
Brilliant:https://brilliant.org/wiki/hensels-lemma/










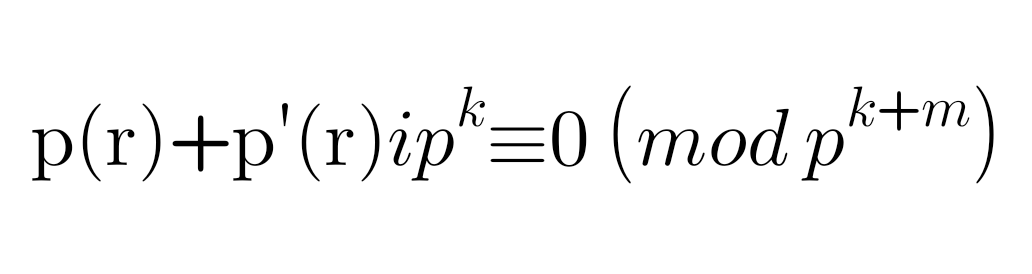








0 Comentarios